플로이드 워셜 알고리즘(Floyd-Warshall Algorithm)

모든 지점에서 다른 모든 지점까지의 최단 경로를 구하는 알고리즘으로 DP(Dynamic Programming)알고리즘에 속한다

한 지점에서 다른 특정 지점까지의 최단 경로를 구하는 다익스트라(Dijkstra) 알고리즘와 구별되며 플로이드 워셜 알고리즘은 음의 가중치를 가지는 그래프에서도 쓸 수 있다

다만 모든 경로를 지나 원래 지점으로 돌아왔을 때, 최종 비용이 음수가 되는 음수 사이클이 있는 그래프에서는 쓸 수 없다

DP 알고리즘?

노드의 개수가 N개라고 할 때, N번 만큼의 단계를 반복하여 점화식에 맞게 2차원 리스트를 갱신하기 때문에 DP로 볼 수 있다

플로이드 워셜 알고리즘의 점화식은 다음과 같다

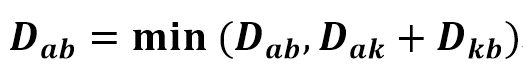
구현 방식(다익스트라와 비교)

다익스트라의 경우 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한 후, 해당 노드를 거쳐가는 경로를 확인하며 최단 거리 테이블을 갱신하는 방식으로 동작

플로이드 워셜 알고리즘 또한 단계마다 '거쳐 가는 노드' 를 기준으로 알고리즘을 수행한다
그러나 매 단계마다 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다!

다익스트라는 한 지점에서 다른 지점까지의 최단 거리를 구하기 때문에 1차원 리스트에 저장한다

플로이드 워셜 알고리즘은 인접 행렬을 이용하여 2차원 테이블에 최단 거리 정보를 저장한다(모든 지점에서 다른 모든 지점까지의 최단 거리를 저장해야 하기 때문)

시간 복잡도

노드의 개수가 N개일 때 N번의 단계를 수행하며, 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐가는 모든 경로를 고려하므로 시간 복잡도는 O(N^3)이다

구현

1. 그래프의 2차원 인접행렬을 만든다. i번째 정점에서 j번째 정점으로 가는 가중치는 D[i][j]이다

2. 만약 i번째 정점에서 j번째 정점이 연결되지 않았다면 무한대 값을 넣는다

3. 인접행렬에서 최단 경로 행렬을 구한다

4. D[i][j] 최단 경로를 저장한다

import java.io.IOException;
import java.util.Arrays;

public class Floyd_Warshall {

    static final int INF = 99999999;

    public static void main(String[] args) throws IOException {
        // 정점의 수 입력
        int N = 4;

        // 인접 행렬 입력
        int[][] D = {{0, 2, 0, 15},
                     {0, 0, 10, 4},
                     {3, 0, 0, 0},
                     {0, 0, 7, 0}};

        // 갈 수 없는 경로 확인
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (i == j) continue;
                if (D[i][j] == 0) D[i][j] = INF;
            }
        }

        // 입력 출력
        System.out.println("=============입력=============");
        for (int[] row : D) System.out.println(Arrays.toString(row));

        // 플로이드 와샬
        for (int k = 0; k < N; k++) {  // 경유 노드 확인
            for (int i = 0; i < N; i++) {  // 출발지
                if (i == k) continue;  // 출발지와 경유지가 같으면 다음 탐색
                for (int j = 0; j < N; j++) {  // 도착지
                    if (j == i || j == k) continue;  // 출발지와 도착지가 같거나 도착지가 경유지이면 다음 탐색
                    D[i][j] = Math.min(D[i][k] + D[k][j], D[i][j]);  // 경유하거나 직접가거나 더 짧은 경로로 대체
                }
            }
        }

        // 결과 출력
        System.out.println("=============결과=============");
        for (int[] row : D) System.out.println(Arrays.toString(row));
    }

}